Notice
Recent Posts
Recent Comments
Link
250x250
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- system
- mysql
- openai
- Algorithm
- Java
- Pipelining
- AI
- DB
- function
- DS
- react
- CSS
- for
- architecture
- instruction
- XML
- python
- html
- javascript
- web
- control
- github
- DATAPATH
- MIPS
- computer
- php
- Rag
- Linux
- Class
- data structure
Archives
- Today
- Total
YYYEJI
[Algorithm] 마스터 정리 (Master Theorem) 본문
728x90

마스터 정리 (Master Theorem)란?
T(n)=aT(n/b)+f(n) 형식의 재귀적인 알고리즘을 계산하기 위한 방법입니다.
① If f(n) = O(nˡºᵍ𝚋ª⁻ᵋ) Ɛ>0, then T(n) = θ(nˡºᵍ𝚋ª).
② If f(n) = θ(nˡºᵍ𝚋ª), then T(n) = θ(nˡºᵍ𝚋ªlg n).
③ If f(n) = Ω(nˡºᵍ𝚋ª⁺ᵋ) Ɛ>0 and a f(n/b) ≤ c f(n), T(n) = θ(f(n))

문제를 풀면서 이해를 해보도록 하겠습니다.
Excercise 1: T(n) = 4T(n/2) + n
T(n)=aT(n/b)+f(n)을 보면 a = 4, b = 2, f(n) = n임을 알 수 있습니다.

Case 1에 만족함을 확인했습니다.
Excercise 2: T(n) = 4T(n/2) + n
T(n)=aT(n/b)+f(n)을 보면 a = 4, b = 2, f(n) = n²임을 알 수 있습니다.
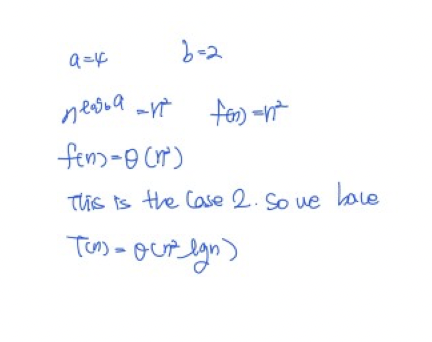
Case 2에 만족함을 확인했습니다.
Excercise 3: T(n) = 4T(n/2) + n
T(n)=aT(n/b)+f(n)을 보면 a = 4, b= 2, f(n) = n³임을 알 수 있습니다.
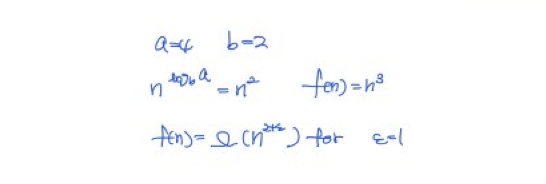
Case 3번은 조건을 하나 더 확인해 줘야 됩니다.
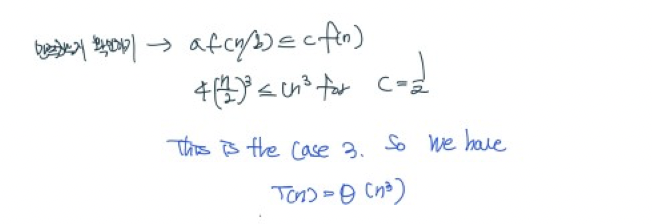
Case 3에 만족함을 확인했습니다.
◡̈
728x90
'Algorithm' 카테고리의 다른 글
| [Algorithm] Greedy로 Huffman code 풀기 (0) | 2023.04.18 |
|---|---|
| [Algorithm] DP로 MCM(Matrix-Chain Multiplication) 풀기 (0) | 2023.04.16 |
| [Algorithm] 재귀 트리(Recursion Tree Theorem) (0) | 2023.04.16 |
| [Algorithm] 점근적 표기법(Asymptotic notation) 이해하기 (0) | 2023.04.16 |
| [Algorithm] 시간복잡도(Time complexity)란? (0) | 2023.04.16 |




