| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- react
- DATAPATH
- control
- DB
- system
- python
- MIPS
- php
- Java
- DoM
- XML
- architecture
- while
- computer
- DS
- html
- web
- function
- Algorithm
- CSS
- MacOS
- data structure
- mysql
- for
- Linux
- instruction
- github
- Class
- Pipelining
- javascript
- Today
- Total
YYYEJI
[MIPS] Floating point number in MIPS 본문

IEEE (Institute of Electrical and Electronics Engineers) 에서는 F.P에 대한 표준 format을 가지고 있습니다.
Machine code로 F.P를 표현하기 위해서 IEEE 754 format을 사용합니다.
(2진수로 부동소수점으로 표현하라는 의미입니다.)
왜 필요할까요?
① Fraction 표현
Ex) 3.1416 . . .
② 매우 작은 숫자를 표현
Ex) .000000001
③ 매우 큰 숫자를 표현
Ex) 3.12345 x 10^n
하기 위해서 입니다.
Format을 알아봅시다.
① Scientific notation
coefficient X (base number) ^ exponent
Ex) 7.1234 X 10^4 , 0.1234 ^ 10^9
② Normalized scientific notation
0 < coefficient < 10
coefficient의 범위가 1~9여야 유효합니다.
Ex) 7.1234 X 10^4 , 3.14 ^ 10^9
Note) Binary의 경우는 0과 1만 사용할 수 있기 때문에 1을 적어야 됩니다.
Normalized scientific notation에 대해서 더 자세히 알아봅시다.
10진수 Floating point
(-1)^sign X sign우리가 표현할 수 있는 범위의 floating point가 너무 크면 overflow
너무 작으면 underflow인데 underflow는 정확성이 요구돼서 우리가 표현할 수 없습니다.
IEEE 754 floating point standard: Coefficient X (base number)^exponent
| sign | exponent | significand |
| 1 bit | 8 bits | 23 bits |
✓ Exponent의 bit 수가 증가하면 표현할 수 있는 범위(range) ↑↑↑
✓ Significand의 bit 수가 증가하면 수의 정확도(accuracy) ↑↑↑
2진수 Floating point
✓ Binary floating point에서 coefficient 부분은 1이기 때문에 생략합니다.
✓ Exponent의 경우 biased number(bias of 127)을 빼줘야 됩니다.
IEEE 754 floating point standard: (-1)^sign X (1+faction) X 2^exponent-bias
| sign | exponent | Fraction |
| 1 bit | 8 bits | 23 bits |
OVERFLOW & UNDERFLOW

우리가 표현할 수 있는 범위의 floating point가 너무 크면 overflow
너무 작으면 underflow인데 정확성이 요구돼서 우리가 표현할 수 없습니다.
기본적인 F.P. addition 순서
Q) 1.000 X 2^-1 + -1.110 X 2^-2
① Binary point를 맞춥니다.
1.000 X 2^-1 + -1.110 X 2^-2
↓
1.000 X 2^-1 + 0.111 X 2^-1
(더 큰 exponent에 맞춥니다.)
② Significands를 더합니다.
1.000
+ -0.111
--------------
를 하기 위해서는 음수를 양수로 변환해줘야 됩니다.
2's complete를 해서 +로 변환해 줍니다.
-00.111 → 11.000 → 11.001
01.000
+ 11.001
--------------
00.001
③ Normalize를 하면서 over/underflow를 체크합니다.
00.001 X 2^-1
↓
1.000 X 2^-4
✓ Exponent가 8bits 넘으면 overflow 입니다.
④ 필요하면 round를 합니다.
1.000 X 2^-4 = 0.0625
예제를 살펴봅시다.
Example 1 ) Represent -3.3212
① Sign bit은 음수이기 때문에 1입니다.
② 3을 2진수로 표현합니다.
8 4 2 1
0 0 1 1
11.~~
③ Fraction 부분을 2진수로 표현합니다.
0.3212
0.5 0.25 0.125. 0.0625 0.03125
~~.0101
④ Nomarlize를 시켜줍니다.
(소수점 왼쪽 부분은 "1" 하나로 맞추는 작업입니다.)
11.0101 * 2^1
= 1.10101
소숫점이 오른쪽으로 가면 2^-1
소숫점이 왼쪽으로 이동하면 2^1
⑤ Exponent 부분에 127(bias number)을 더해줍니다.
1+127 = 128
10진수: 128
2진수: 100000000
⑥ 결과를 합쳐봅니다.
- 1.10101 X 2^1
⑦ IEEE 754 format을 통해서 나타내줍니다.
| sign | exponent | fraction |
| 1 | 10000000 | 101010........0 |
✓ fraction 부분에서 . 왼쪽 부분은 생략합니다.
✓ 이유는 .왼쪽 뿐은 무조건 1이기 때문입니다 → Implied
Example 2) 1 10000001 01000....00 to Decimal number
① 처음에 bit 1은 음수임을 나타냅니다.
② 10000001는 exponent이며 10진수로 나타내면 129입니다.
여기서 127(bias number)을 빼줘야 됩니다.
Exponent: 129-127 = 2
③ Fraction 부분은 .01은 0.25을 나타냅니다.
0.5 0.25 0.125
0 1 0
④ 지금까지 구한 숫자들을 한 번에 나타냅니다.
-1.25 X 2^2
⑤ 4번을 계산해주면 끝입니다.
-1.25 X 2^2 = -5.0
Example 3)
1 - Represent -12.75 with IEEE 754 floating-point single precision standard representation.
2 - Add 1.01010 X 2^4 to 1.00111 X 2^6, Do we need guard/round bit? Assume significand is 5-bits long.
3 - Multiply 1.010X2^4 to 1.001X2^6
↓↓↓ Solution ↓↓↓

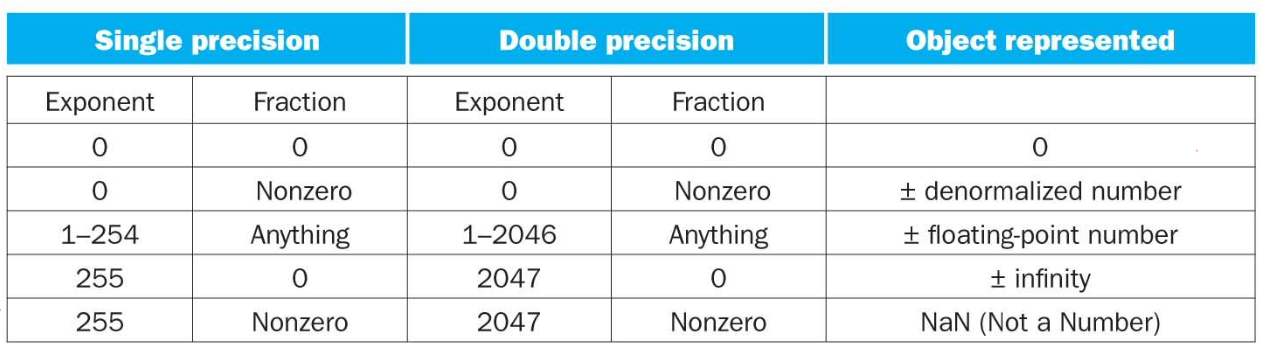
Summary
◡̈
'Computer architectures' 카테고리의 다른 글
| [MIPS] D-latch란? (0) | 2022.10.30 |
|---|---|
| [MIPS] Combinational circuit과 Sequential circuit의 차이점 (0) | 2022.10.29 |
| [MIPS] Division in MIPS (0) | 2022.10.20 |
| [MIPS] Multiplication in MIPS (0) | 2022.10.20 |
| [MIPS] 1부터 N 사이의 3의 배수의 합을 구하는 assembly code (0) | 2022.10.20 |




