| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- for
- python
- system
- architecture
- DS
- html
- CSS
- instruction
- computer
- Class
- MacOS
- function
- DB
- DoM
- Linux
- Algorithm
- Java
- mysql
- php
- while
- DATAPATH
- github
- data structure
- XML
- control
- web
- javascript
- MIPS
- Pipelining
- react
- Today
- Total
YYYEJI
[DS] 깊이 우선 탐색(DFS)이란? 본문

하나의 vertax로부터 모든 vertex를 한 번씩 방문하는 그래프 탐색이 있습니다.
↓↓↓ 그래프란? ↓↓↓
https://yyyeji.tistory.com/378
[DS] 그래프(Graphs)의 종류와 관련 용어
그래프(Graphs)란? 객체 사이의 연결 관계를 나타낼 수 있는 자료 구조입니다. 그래프(graph)는 vertax의 집합과 edge의 집합으로 이루어집니다. - vertax = {a, b, c, d, e} - edge = {(a, b), (a, e), (b, c), (c, d), (c, e
yyyeji.tistory.com
아래에 DFS 방문 예제와 코드가 있습니다.
깊이 우선 탐색(Depth First Search)이란?
그래프 탐색에서 깊은 부분을 먼저 탐색하는 알고리즘이며,
재귀함수(recursion)이나 스택(stack)을 사용합니다.
↓↓↓ 스택(stack)? ↓↓↓
https://yyyeji.tistory.com/360
[DS] 스택(Stack)이란?
스택(Stack)이란? LIFO(Last in First out) 특성을 가지는 linear list입니다. Linear list의 한쪽 끝위치(TOP)에서 Push와 Pop이 이뤄집니다. (즉, stack에서 pop을 하면 그 원소가 가장 마지막에 넣은 원소입니다.) Sta
yyyeji.tistory.com
장점(Adventage)
경로(path)에 있는 vertex만 생각하면 되기 때문에 저장공간이 비교적 적고,
찾고자 하는 vertex가 깊이 있는 경우에 해를 빠르게 구할 수 있습니다.
알고리즘(Algorithm)
① 시작할 vertex를 방문하고, 스택(stack)에 넣는다.
② 스택(stack)에 top 원소와 인접한 vertex 중 아직 방문하지 않은 vertex를 한 개 선택하여 방문하고 스택(stack)에 넣는다.
③ 더 이상 선택할 원소가 없다면, 스택(stack)에서 원소 하나를 제거(pop)합니다.
스택(stack)이 빈(empty) 상태일 때까지 ②~③번을 반복합니다.
아래 그래프의 모든 vertex를 깊이 우선 탐색을 통해 방문해 보겠습니다.
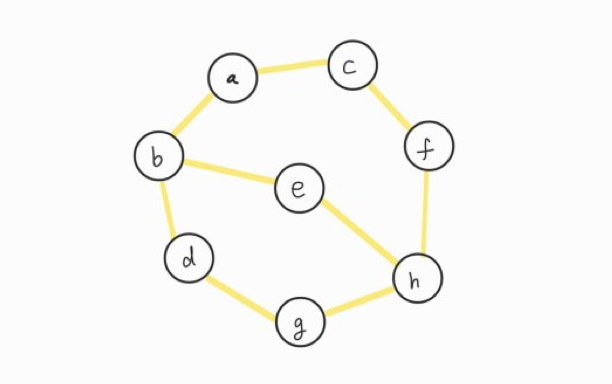
ⓐ를 시작 vertex로 두겠습니다.
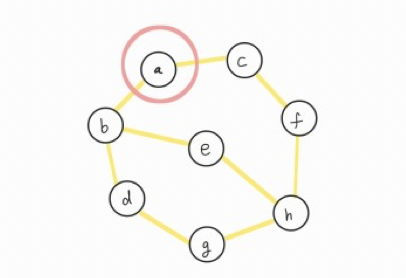
| ⓐ | ← Start vertax and Top element |
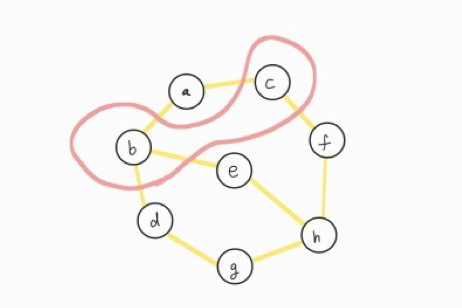
ⓐ에서 방문할 수 있는 vertex는 ⓑ, ⓒ입니다.
어디로 갈지는 직접 정해주면 됩니다.
저는 ⓑ로 가겠습니다.
ⓑ를 방문하고 스택(stack)에 넣어줍니다.
| ⓑ | ← Top element |
| ⓐ |
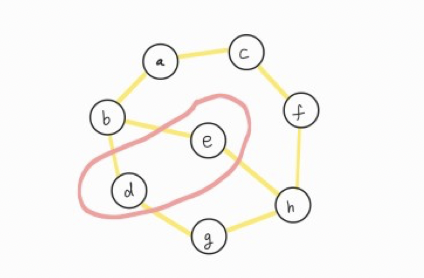
ⓑ에서 방문할 수 있는 vertex는 ⓓ, ⓔ입니다.
ⓓ를 방문하고 스택(stack)에 넣겠습니다.
| ⓓ | ← Top element |
| ⓑ | |
| ⓐ |
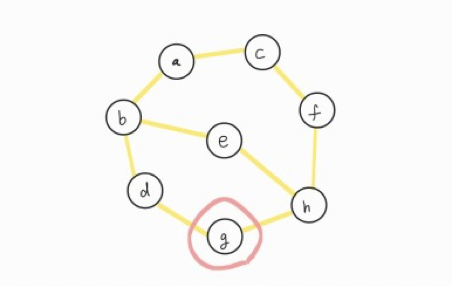
ⓓ에서 방문할 수 있는 vertex는 ⓖ이기 때문에 ⓖ를 방문하고 스택(stack)에 넣어줍니다.
| ⓖ | ← Top element |
| ⓓ | |
| ⓑ | |
| ⓐ |
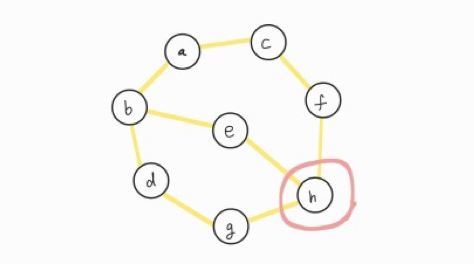
다음으로 ⓗ에 방문하고 스택(stack)에 넣어줍니다.
| ⓗ | ← Top element |
| ⓖ | |
| ⓓ | |
| ⓑ | |
| ⓐ |
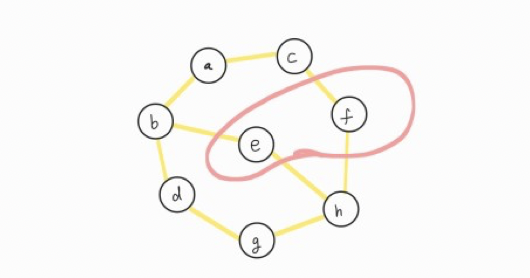
ⓗ는 ⓔ, ⓕ를 방문할 수 있습니다.
ⓔ를 먼저 방문하겠습니다.
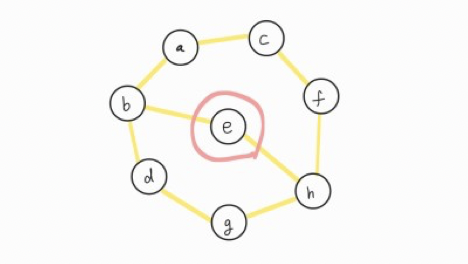
| ⓔ | ← Top element |
| ⓗ | |
| ⓖ | |
| ⓓ | |
| ⓑ | |
| ⓐ |
ⓔ는 이미 방문된 ⓑ, ⓗ만 연결되어 있기 때문에,
top 원소를 하나 제거(pop)해줍니다.
| ⓗ | ← Top element |
| ⓖ | |
| ⓓ | |
| ⓑ | |
| ⓐ |

ⓗ에서 갈 수 있는 vertex는 ⓕ가 남아있기 때문에 ⓕ를 방문하겠습니다.
| ⓕ | ← Top element |
| ⓗ | |
| ⓖ | |
| ⓓ | |
| ⓑ | |
| ⓐ |
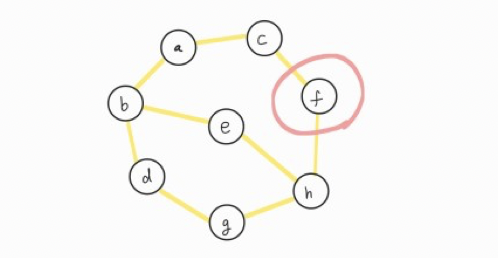
ⓕ에서는 ⓒ는 아직 방문하지 않았기 때문에,
ⓒ에 방문하고 스택(stack)에 넣겠습니다.
| ⓒ | ← Top element |
| ⓕ | |
| ⓗ | |
| ⓖ | |
| ⓓ | |
| ⓑ | |
| ⓐ |
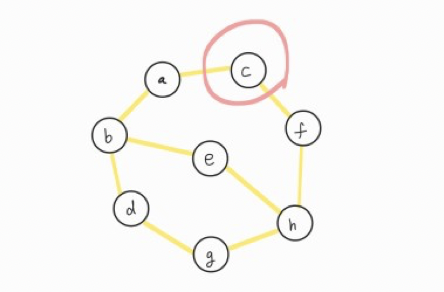
이제 모든 vertex를 방문했기 때문에 스택(stack)에 남아있는 원소를 모두 제거(pop)하면 됩니다.
재귀함수 함수 구현
#include <iostream>
#include <vector>
using namespace std;
bool visited[8];
vector<char> graph[8];
void dfs(char x){
if(visited[x]) return;
visited[x] = true;
cout << x << " ";
for(int i = 0; i<graph[x].size(); i++){
char y = graph[x][i];
dfs(y);
}
}visited[8]는 vertex 방문 여부를 위한 배열입니다.
vector<char> graph[8]은 그래프의 정보를 담고 있을 벡터(vactor)입니다.
사용자 정의 함수인 dfs()를 살펴보겠습니다.
if(visited[x]) return;
파라미터(parameter)로 들어온 문자의 방문 여부를 확인해 줍니다.
이미 방문된 곳이라면 아무런 수행 없이 그대로 return 합니다.
방문되지 않았다면 다음 코드를 수행합니다.
visited[x] = true;
파라미터(parameter)로 들어온 문자의 vertex를 지금 방문했기 때문에 visited를 true로 바꿉니다.
cout << x << " ";
방문된 vertex를 출력합니다.
for(int i = 0; i<graph[x].size(); i++) {
한 vertex에 연결된 다른 vertex에 모두 방문하게 됩니다.
int y = graph[x][i];
다음으로 방문될 vertex를 구해주고,
dfs(y);
모든 vertex에 방문할 때까지 반복합니다.
Note) 방문 여부를 체크하지 않으면 무한 루프에 빠질 수 있다.
main 함수 구현
int main() {
graph['a'].push_back('b');
graph['a'].push_back('c');
graph['b'].push_back('a');
graph['b'].push_back('d');
graph['b'].push_back('e');
graph['c'].push_back('a');
graph['c'].push_back('f');
graph['d'].push_back('b');
graph['d'].push_back('g');
graph['e'].push_back('b');
graph['e'].push_back('h');
graph['f'].push_back('c');
graph['f'].push_back('h');
graph['g'].push_back('d');
graph['g'].push_back('h');
graph['h'].push_back('g');
graph['h'].push_back('e');
graph['h'].push_back('f');
dfs('a');
return 0;
}

위에서 풀었던 DFS 예제와 같이 그래프를 생성해주었습니다.
main 함수를 실행하면 아래와 같은 벡터(vector)가 생성됩니다.

위에 있는 예제와 같이 따라갔을 때 결과가 잘 출력된 것을 확인할 수 있습니다.
↓↓↓ 다른 그래프 탐색 방법 공부하기 ↓↓↓
https://yyyeji.tistory.com/380
[DS] 넓이 우선 탐색(BFS)이란?
하나의 vertax로부터 모든 vertex를 한 번씩 방문하는 그래프 탐색이 있습니다. ↓↓↓ 그래프란? ↓↓↓ https://yyyeji.tistory.com/378 [DS] 그래프(Graphs)의 종류와 관련 용어 그래프(Graphs)란? 객체 사이의
yyyeji.tistory.com
◡̈
'Data structure' 카테고리의 다른 글
| [DS] 최소 신장 트리(Minimum Spanning Tree)란? (0) | 2023.01.24 |
|---|---|
| [DS] 넓이 우선 탐색(BFS)이란? (2) | 2023.01.05 |
| [DS] 그래프(Graphs)의 종류와 관련 용어 (0) | 2023.01.05 |
| [DS] 이진탐색트리(Binary Search Tree)란? (2) | 2023.01.04 |
| [DS] 힙(Heap)이란? (0) | 2023.01.03 |




