Python
[Python] 집합(Set) 정리
YEJI ⍢
2022. 10. 6. 17:01
728x90

집합(Set)은
순서가 없고, 집합안에 특별한 원소를 가집니다.
Mutable 객체입니다.
아래와 같이 사용합니다.
s = {'A', 'B', 'C'}
print(type(s))
특별한 원소를 가진다고 했던 것처럼 중복된 값은 자동으로 삭제됩니다.
s = {'A', 'B', 'C', 'a', 'A'}
print(s)
Set은 순서가 없기 때문에 어떤 원소가 먼저 나올지는 모릅니다.


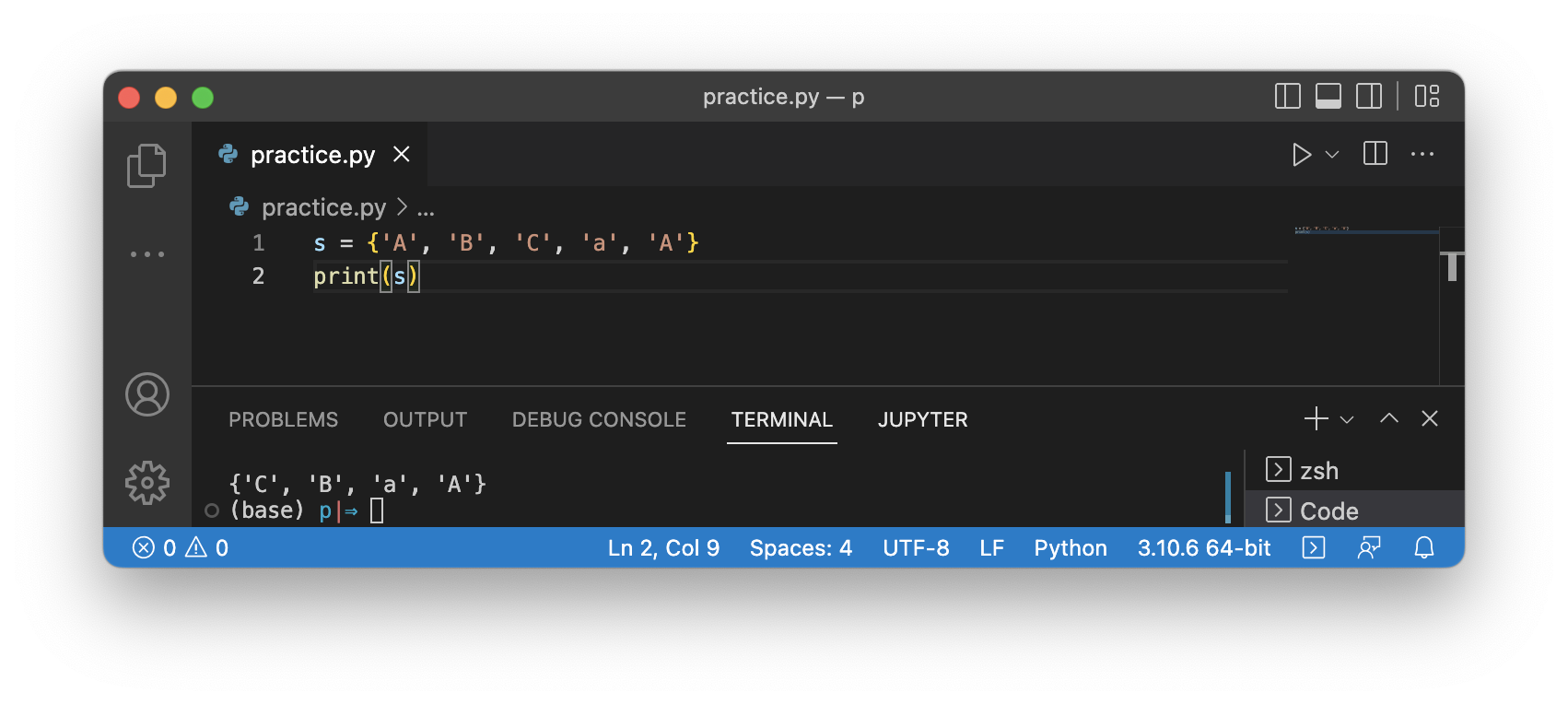
↑↑↑ 여러 번 실행했을 때 나오는 결과가 다르다는 것을 확인할 수 있습니다 ↑↑↑
원소가 튜플 안에 존재하는지도 확인할 수 있습니다.
s = {'A', 'B', 'C', 'a', 'A'}
print('A' in s)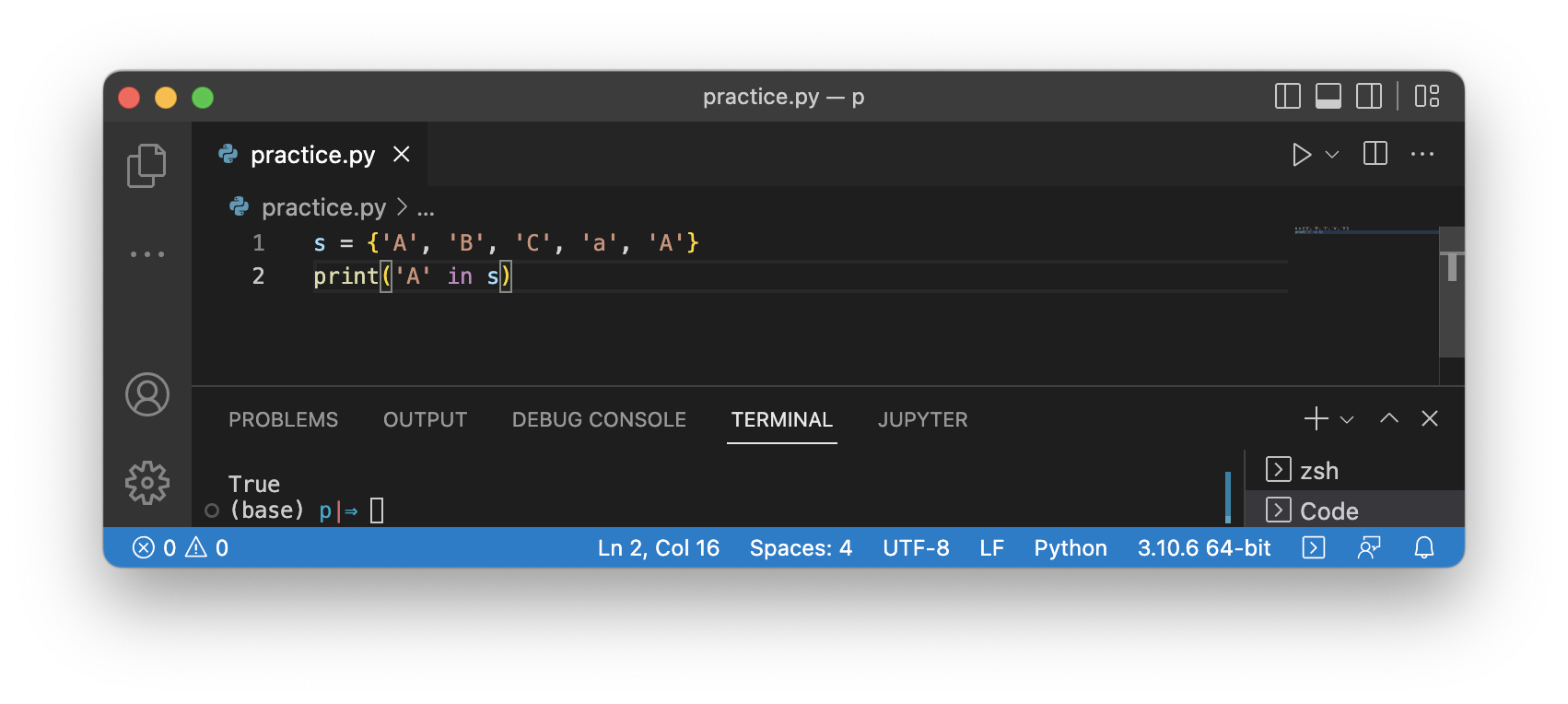
s = {'A', 'B', 'C', 'a', 'A'}
print('D' in s)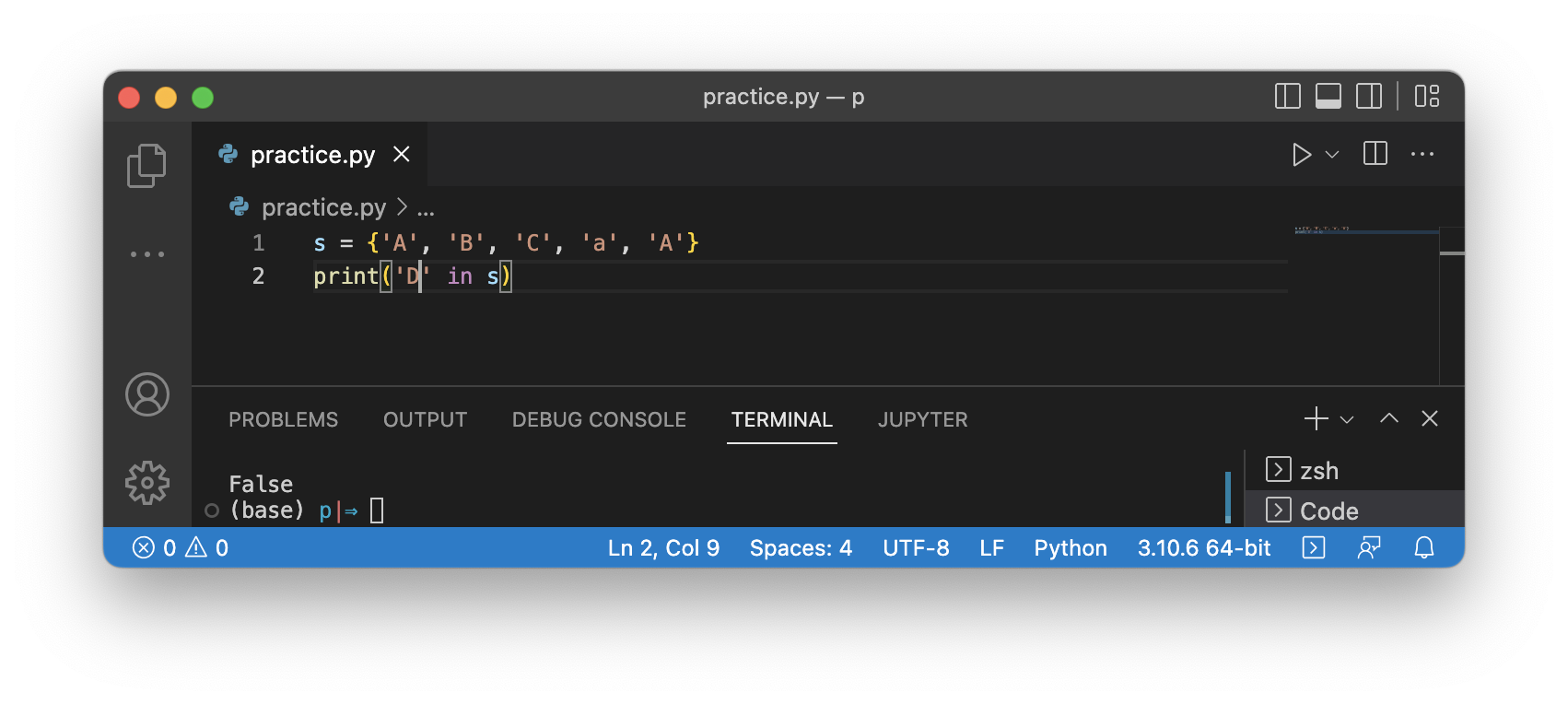
'add' method - 하나의 원소 추가
s = {'A', 'B', 'C', 'a', 'A'}
s.add('D')
print(s)
'update' method - 여러 개의 원소 추가
s = {'A', 'B', 'C', 'B'}
s.update(['D', 'A', 'E', 'F'])
print(s)
'remove' method - 원소 삭제
s = {'A', 'B', 'C', 'a', 'A'}
s.add('D')
s.remove('a')
print(s)
'copy' method - 튜플 복사
s = {'A', 'B', 'C', 'B'}
sc = s.copy()
print(sc)
' | ' operation - 합집합
s1 = {'A', 'B', 'C', 'D'}
s2 = {'A', 'E'}
print(s1|s2)
' & ' operation - 교집합
s1 = {'A', 'B', 'C', 'D'}
s2 = {'A', 'E'}
print(s1&s2)
' - ' operation - 차집합
s1 = {'A', 'B', 'C', 'D'}
s2 = {'A', 'E'}
print(s1-s2)
' ^ ' operation - 대칭차집합 (합집합 - 교집합)
s1 = {'A', 'B', 'C', 'D'}
s2 = {'A', 'E'}
print(s1^s2)
'union' method - 합집합
s1 = {'A', 'B', 'C', 'D'}
s2 = {'A', 'E'}
s3 = s1.union(s2)
print(s3)
'intersection' method - 교집합
s1 = {'A', 'B', 'C', 'D'}
s2 = {'A', 'E'}
s3 = s1.intersection(s2)
print(s3)
'difference' method - 차집합
s1 = {'A', 'B', 'C', 'D'}
s2 = {'A', 'E'}
s3 = s1.difference(s2)
print(s3)
'symmetric_difference' method - 대칭차집합 (합집합 - 교집합)
s1 = {'A', 'B', 'C', 'D'}
s2 = {'A', 'E'}
s3 = s1.symmetric_difference(s2)
print(s3)
'issubset' method - 부분집합 여부 확인
s1 = {'A', 'B', 'C', 'D'}
s2 = {'A'}
print(s2.issubset(s1))
print(s1.issubset(s2))
'issuperset' method - issubset과 반대 superset인지 확인
s1 = {'A', 'B', 'C', 'D'}
s2 = {'A'}
print(s1.issuperset(s2))
print(s2.issuperset(s1))
'isdisjoint' method - 교집합이 없으면 True, 있으면 False
s1 = {'A', 'B', 'C', 'D'}
s2 = {'E','F'}
print(s1.isdisjoint(s2))
◡̈